What Happens When I Change The Slope Of Curves Plot In Photoshop Cs6

What is a Gradient? Contents (Click to skip to that department):

Definition
"Ascent Over Run"
Formula for a Straight Line
Find the slope with algebra

More Advanced Topics:

Slope of a Curve
Slope of a Tangent Line (Using the Definition of a Limit)
What is a Slope Field?

i.What is a slope?

The word "gradient" in math has roughly the same meaning in math as it has in everyday language:

"…a surface of which one stop or side is at a higher level than another; a ascension or falling surface."

It's slightly more defined when used in math; information technology's a number that describes both the direction (positive or negative) and the steepness of the line. It's usually denoted by the letter of the alphabet m.

two. "Ascent over Run"

what is a slope?

Informally, the slope of a line is found with the catchy phrase "rise over run". This works with whatsoever segment, of any length, for any directly line:

Find the ascension (the length of a segment on the y-axis): The rise (the length of the vertical blue line) in the above picture is 4.
Find the "run" (the length of a segment on the ten-axis): The run (the length of the horizontal bluish line) is 2.
Separate the rise (Step 1) past the run (Step 2): 4/ii = ii.

The slope for this example is 2.

three. Formula for a Straight Line

The formula for a straight lineis:
slope formula

Where:

b = the y-intercept (where the graph crosses the y-centrality),
thousand = the slope (i.eastward. how steep the line is),
x = a variable.

formula for slope

The equation for a straight line (more than formally chosen a "linear equation") is pretty straightforward to use if you're given a set of points (example 1). You lot might also be asked what the slope is for something similar y = -nine (example ii) or x = -2.5 (case 3). Although they are both equations (and you might think that y = mx + b will help), you really need the formula to visualize the reply.*
Examples:

The slope of the points (two,1) and (4,2) is one/2 considering: (y₂ – y₁) / (ten₂ – x₁) = (2 – 1) / (iv – 2) = 1/2.
The slope of y = ix is cypher. The graph of y = ix is parallel to the x-axis and is flat (i.e. it doesn't ascent or autumn at all). You could use the formula to piece of work this out by choosing a couple of random x-values (I'm going to pick 2 and 3):
g = (y₂ – y₁) / (10₂ – 10_i)
= (nine – 9)/(2 – 1) = 0 / 1 = 0.
Every bit the y-values are abiding and will always equal zero when subtracted (i.e. 10 – 10, iv – 4, -three – -3), the slope of a line with the equation y = "whatever number" will e'er be naught.
The gradient of x = 5 is undefined. Any line with an equation of x = "any number" is going to exist undefined because wait what happens when you plug a couple of points (any random points) into the formula:
m = (2 – ane) / (five – 5) = 1 / 0 = division by nix is undefined.

*That said, technically yous could but memorize that equations with the grade y = "whatsoever number" has a gradient of zero and 10 = "any number" has an undefined gradient.

4. Detect the Slope with Algebra

The basic formula for a linear equation is y = mx + b, where "chiliad" is the gradient. If you're given the formula and need to find one thousand, you may need to:

Await at the formula to find it (example 1),
Use a little algebra to get the equation in the right grade (example 2).

Examples:

The slope of y = 210 + v is 2.
The slope of 3y – 9x = 12 is 3, because if nosotros rearrange the formula to look like y = mx + b we go:
Adding 9x to both sides: 3y = 9x + 12.
Dividing by iii (both sides): y = 3x + 4.

Tip: if there's zip before the x (i.e. y = x + 2), the slope is one, considering ane*x = x.

2. Basic Slope Formula: k = ascent/run = (y₂ – y_ane) / (x_two – x₁).

5. What is a Slope? The Slope of a Curve

The main divergence between the slope of a directly line and the slope of a curve is that the slope of a straight line remains constant while the slope of a curve changes betwixt points.

How can we determine what the slope of a curve is if the values are constantly changing? We can do that by using a tangent line. A tangent line is a straight line that touches the plotted bend at a single point. That bespeak is known as the point of tangency.

slope of a curve

The tangent line is the pocket-size red line at the top of the illustration. Notice how it touches the curved line at a single point.

Formula for Slope of a Curve

The gradient of a linear equation can exist found with the formula: y = mx + b. When dealing with a curved line, where the slope is irresolute, yous can't use the same formula. You have to divide the change in y-values by the change in x-values, represented as:

g = modify in y/change in x

In order to utilise this formula to notice the slope of a curve, select two points to plug into the formula. Let's look at an example.

Instance question: Find m at the point (ix, 3).
In the graph above the tangent line is again fatigued in red. The tangent touches the curve at (ii.3, 5). Once we take the point from the tangent it is just a matter of plugging the values into the formula.

m = (9-5)/(3-2.3) = 4/.7 = v.71.

Thus the slope of the curve at indicate (9, iii) is 5.71.

half dozen. How to Discover the Slope of a Tangent Line using the Definition of a Limit

There are several ways to find the slope of a tangent line. The usual way is to take the derivative—It'southward equal to the slope of the tangent line at any point. However, if yous're asked to use the 'definition of a limit', chances are you haven't yet covered how to take a derivative yet in your course. The formal definition of the limit can be used to discover the gradient of the tangent line:
If the point P(ten₀,y₀ ) is on the curve f, then the tangent line at the point P has a slope given by the formula:
M_tan = lim _h→0 f(x₀ + h) – f(x₀)/h.

Example question: Find the slope of the tangent line to the curve f(10) = 2x² + 3x – 4 passing through the signal P(-1, 5).

Step ane: Replace the "x" in your original role by 10 + h in the first office of the definition of the limit:
g_tan = lim _h→0 [two ( x + h )^two ] + 3(x + h) + 4]

Step 2: Subtract your original function and split up past h (all yous are doing here is completing the definition for the limit):
m_tan = lim _h→0 [2 ( x + h )² + three(10 + h) – 4] – [2x^two + 3x – 4 ] / h

Stride 3: Solve using algebra. The entire purpose of the post-obit steps is to remove the "h" from the denominator to prevent sectionalisation by zilch:

FOIL the first part, (x+h)²:
m_tan = lim _h→0 [ii(ten² + 2hx + hⁱⁱ] + 3(x + h) – iv] – [2x^two + 3x – 4 ] / h
Multiply out iii(x + h):
m_tan = lim _h→0 [two(x² + 2hx + h^two] + 3x + 3h – iv] – [2x² + 3x – 4 ] / h
Distribute the negative sign
m_tan = lim _→0 [2(10² + 2hx + h²] + 3x + 3h – 4] – 2x² – 3x + 4 / h
Distribute the leading 2:
m_tan = lim _h→0 [2xⁱⁱ + 4hx + 2h² + 3x + 3h – iv – 2x^two – 3x + iv] / h
Cancel out terms (-3x, -2x², -four)
1000_tan = lim _h→0[4hx + 3h ² + 3h ] / h
Factor the "h" out:
k_tan = lim _h→0 h (4x + 2h + 3) / h
= lim _h→0 4x + 2h + 3
Set the "2h" to zero (considering yous are taking the limit, "h" is insignificant). In other words, delete information technology:
= lim _h→0 4x + 3

This gives you lot the part for the gradient of the tangent line.

Step 4: Insert your signal into the role:
one thousand_tan = 4 (-1) + 3 = -ane
The gradient of the tangent line is -1.

That'southward it!
Back to Top

What is a Slope Field?

A slope field (sometimes called a directional field) represents the solutions to a kickoff order differential equation of a scalar function. A serial of tic marks indicate slope. The terms gradient field and vector field are sometimes used to mean the aforementioned affair, but in that location is an of import difference: All the tic marks in a slope field accept the same length; The marks in vector fields vary in length co-ordinate to the magnitude of the vector.

Essentially, the slope field contains a series of short, bidirectional lines, each 1 unit long, and each showing the tangent line of the function's curve at their center points.

Slope fields are besides sometimes called direction fields, especially if the vectors retain directional arrows.

The image below shows the gradient field of dy/dx = xⁱⁱ – x – ii. 3 functions are represented by different colors:

Blue: y = (x³/3)-(xⁱⁱ/2) – 2x + four,
Red: y = (ten³/iii)-(x^two/two) – 2x,
Turquoise: y = (x³/3)-(x²/2) -2x – four.

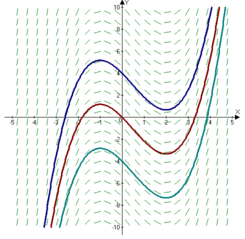
Slope Field

Slope Field Applications

Slope fields of fifty-fifty very complex derivatives can be generated chop-chop and effortlessly by a computer, then they are often used every bit the offset step in understanding a problem earlier a decision is made on procedures to find an exact solution. They requite a good visual understanding of the problem and allow you lot to see the long term behavior of the solution.

They can as well be used every bit a guide to outline possible solutions. In cases where we don't have the actual derivative in manus, they can be used by computers to generate numeric solutions through routines like Euler'due south method or the Runge–Kutta methods.

What is a Slope? References

Barker, Christopher A. A Theoretical Introduction to Slope Fields. Mathematics & Science Learning Center Reckoner Laboratory. San Joaquin Delta Higher. Retrieved from http://calculuslab.deltacollege.edu/ODE/7-1/7-1-0-h.html on Apr half-dozen, 2019.
Kahn, D. Cracking the AP Calculus AB & BC Exams.
Larson & Edwards. Calculus.
Schwartz, Ken. Differential Equations: Slope Field Generator. GeoGebra Retrieved from https://www.geogebra.org/g/MJbBarpr on Apr 6, 2019.

---------------------------------------------------------------------------

Need help with a homework or examination question? With Chegg Study, you can become step-by-footstep solutions to your questions from an expert in the field. Your start 30 minutes with a Chegg tutor is gratuitous!